Research question, hypothesis testing and sample sizes (Continuous data)

Blog
Statistics
Sample Size
Author

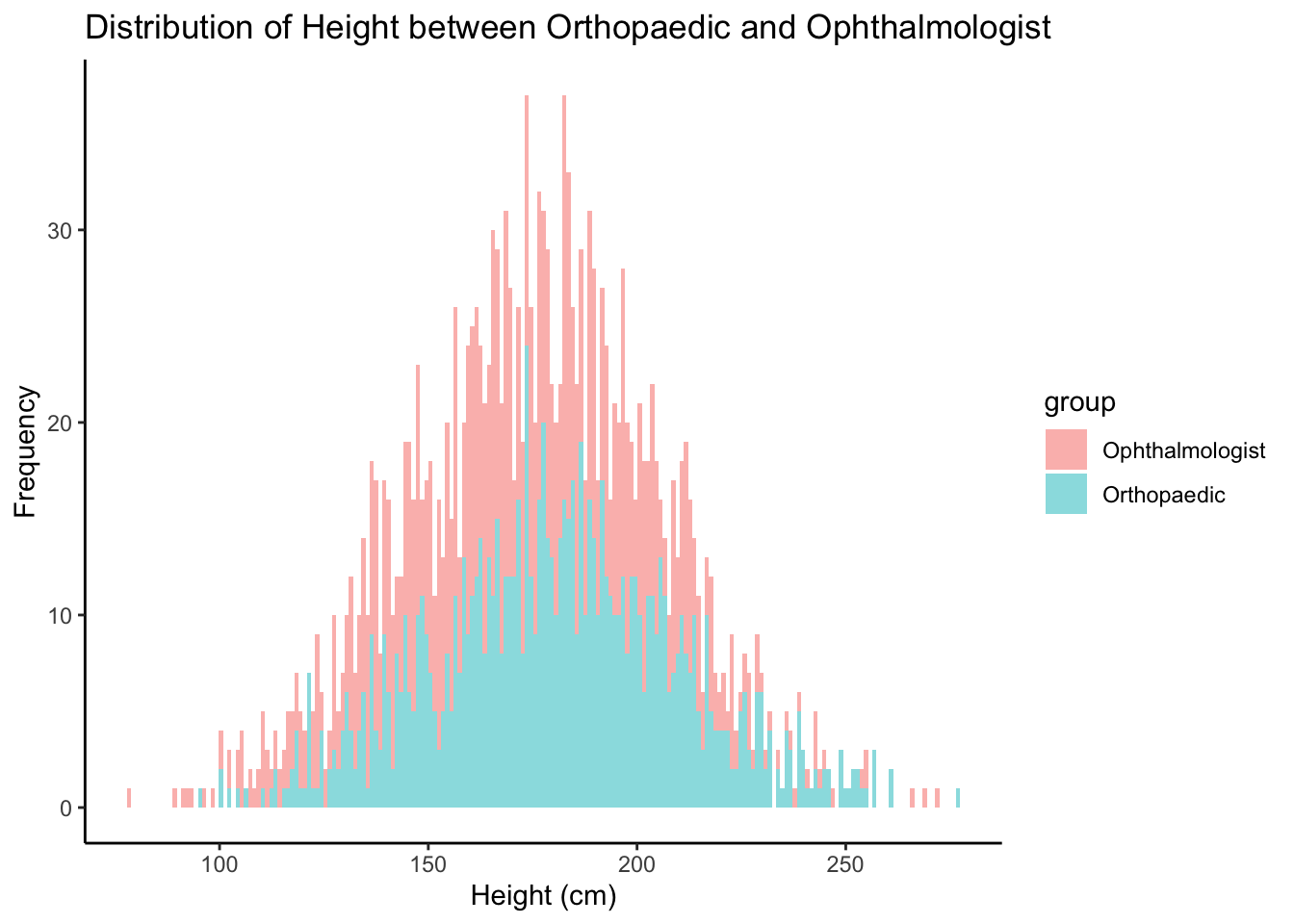
Brian Brummer

Published

February 19, 2025

Research question to Hypothesis to Sample Size

Most research needs to have a research question, which means you have to have a hypothesis to test and sufficient data to demonstrate whether to accept or reject your hypothesis.

A good research question

An effective research question must include:

  • An outcome measure (e.g., weight, height, success, failure, pain score, anxiety score)

  • An exposure or intervention (e.g., surgery, time, diagnosis, treatment)

  • An idea of the direction and magnitude of the difference between the groups (e.g., higher, lower, different)

For example, a simple research question might be:

To determine whether the height (outcome) between orthopaedic surgeons and ophthalmologists (exposure: type of specialty) differs by 10cm (magnitude of difference).

We should keep in mind

  • we can also keep in mind the data types. Briefly, data types can be:
    • Continuous (e.g., height, weight, blood pressure)
    • Categorical (e.g., HIV stage, Death, Complication)

Hypothesis

The null hypothesis (H₀) represents the status quo or the assumption of no difference. To show that there is a difference, you must disprove H₀.

  • Null hypothesis (H₀): The heights are not different by more than 10cm between the two groups.
  • Alternative hypothesis (H₁): The heights are different by more than 10cm.

By disproving H₀, you support H₁.

Sample Size Calculations

A simplified formula for the sample size required for detecting a difference between two means (or continuous variables) is:

\[ n = \frac{\left(Z_{1-\alpha/2} + Z_{1-\beta}\right)^2 \, \sigma^2}{\Delta^2} \]

We need to fill in some values with our best guesses, or info from exisitng literature.

Where:

  • \(( Z_{1-\alpha/2} )\) won’t change and is the critical value for the desired confidence level (e.g., 1.96 for 95% confidence).
  • \(( Z_{1-\beta} )\) won’t change and is the critical value for the desired power (e.g., 0.84 for 80% power).
  • \(( \Delta )\) is the minimum detectable difference (we set this to 10 cm).
  • \(( \sigma )\) is the standard deviation of the outcome.

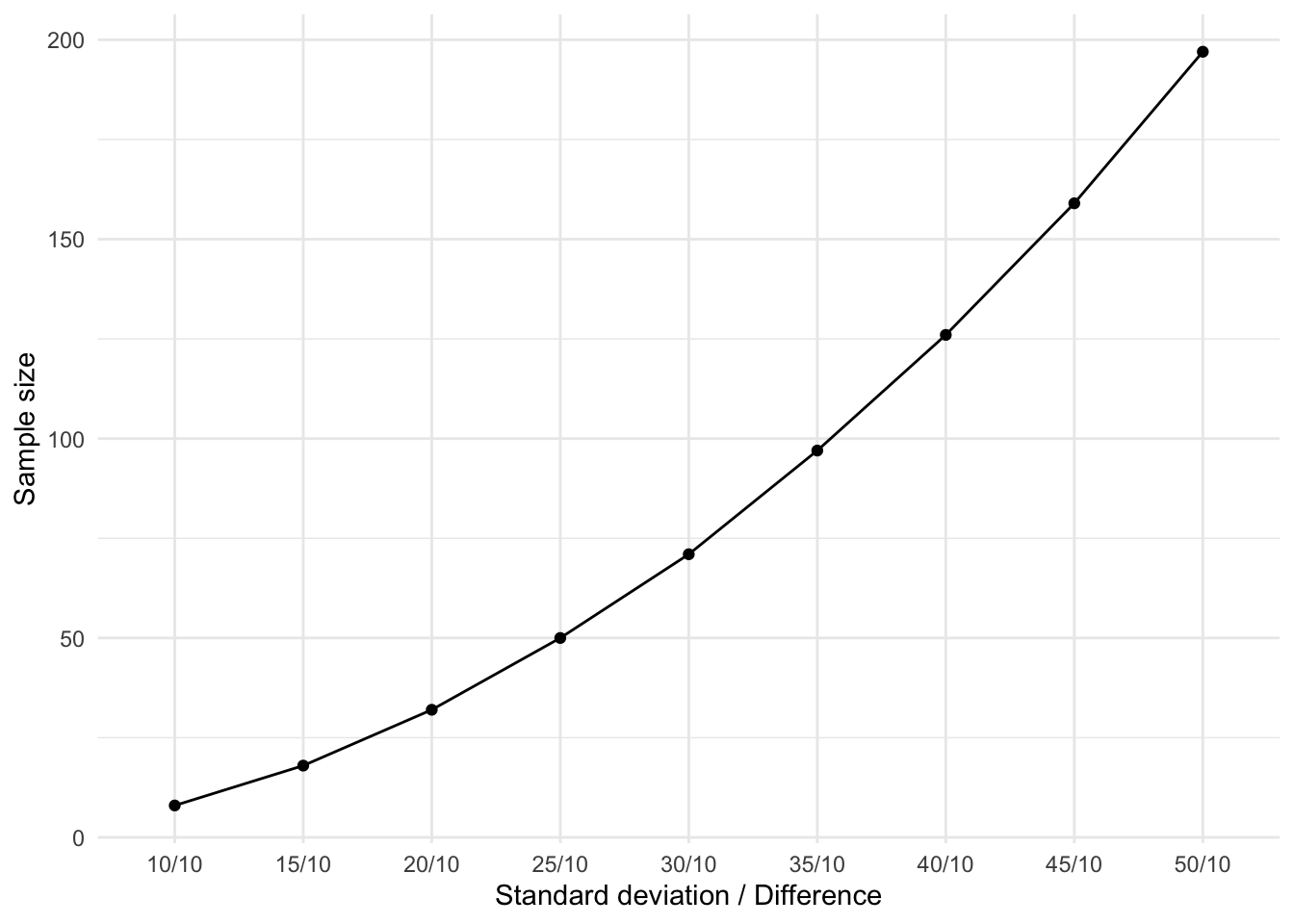
In normal language: We want to show atleast the \(\Delta\) between the two groups. I like to call \(\Delta\) the minimum detectable difference - If the actual difference is smaller than 10cm, we will not be able to detect it.

You must also consider the variability in each group. In other words each persons height will vary, or is spread around the mean. We describe this by the standard deviation (SD) (σ) of the outcome. As a sample size increases, the SD becomes narrower.

SD is calculated by taking the square root of the differences between each value and the mean, squaring them, summing them, and dividing by the number of values.

What will this data look like?

[1] 12.5


     Two-sample t test power calculation 

              n = 142.2462
              d = 0.3333333
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

Finding a difference that is equal to the to or more than the standard deviation is ideal but this is generally not the case in real life, often you may wish to find a smaller difference with a much larger spread of data around a mean. Remember spread (or variance) can be affect by the natural variablitly of the event you are observing or the measurement process itself. Think of how much variation you see in the measuremnts you observe each day, from patietns weight, CD4 count, blood pressure, etc.

In Summary

Research Question: To determine whether the height between orthopaedic surgeons and ophthalmologists differs by 10cm.

Null Hypothesis: The heights are not different by more than 10cm between the two groups.

A p-value of <0.05 means we reject the null hypothesis and accept the alternative hypothesis.

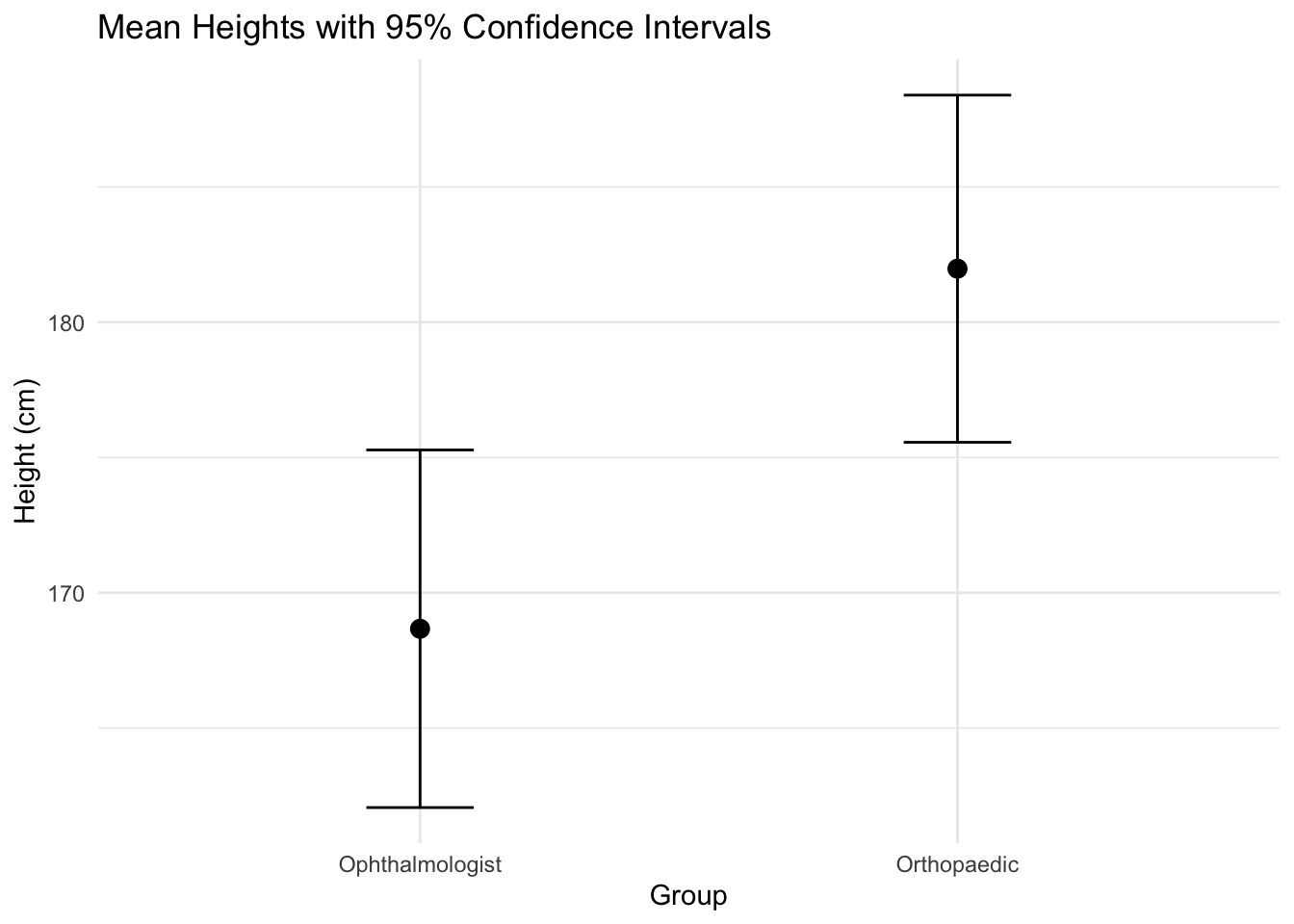
We determined the sample size by calculating the number of participants needed to detect a difference of 10 cm with a power of 80% and a significance level of 5%. Both groups had a standard deviation of 15 cm. This results in a sample size of 142 (or 71 per group).

Characteristic Ophthalmologist
N = 71 (95% CI)1		 Orthopaedic
N = 71 (95% CI)1		 p-value2
height 168 (28) (162, 175) 182 (27) (175, 188) 0.004
Abbreviation: CI = Confidence Interval
1 Mean (SD)
2 Welch Two Sample t-test
../after.html